問題
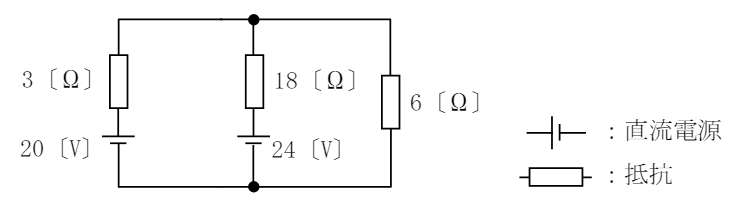
図に示す回路において、6[Ω]の抵抗の両端の電圧の値として、最も近いものを下の番号から選べ。
- 7.2[V]
- 9.6[V]
- 12.0[V]
- 14.4[V]
- 16.8[V]
解答
4
解説
キルヒホッフの法則を使って解きます。
まず、電流を下図のように定義すると、キルヒホッフの第1法則より、下記の関係式が成り立ちます。
$$\begin{eqnarray} I_1=I_2+I_3 \tag{1} \end{eqnarray}$$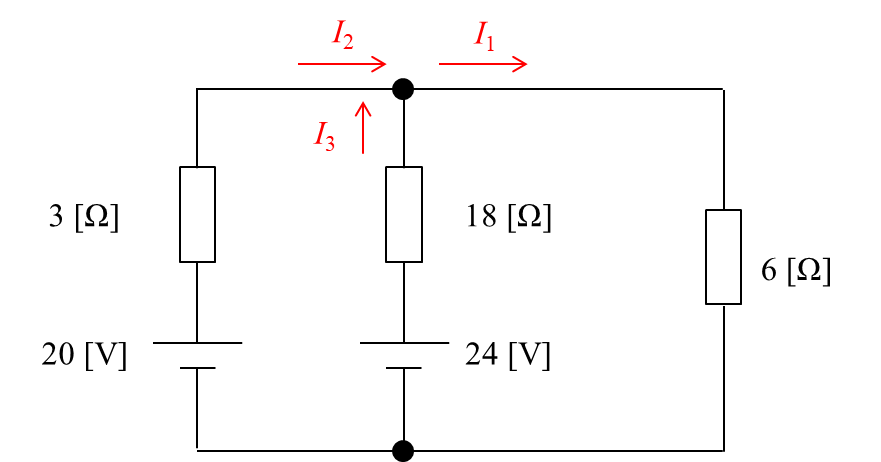
続いて、閉回路を①、②のように定義すると、キルヒホッフの第2法則より、下記の関係式が成り立ちます。
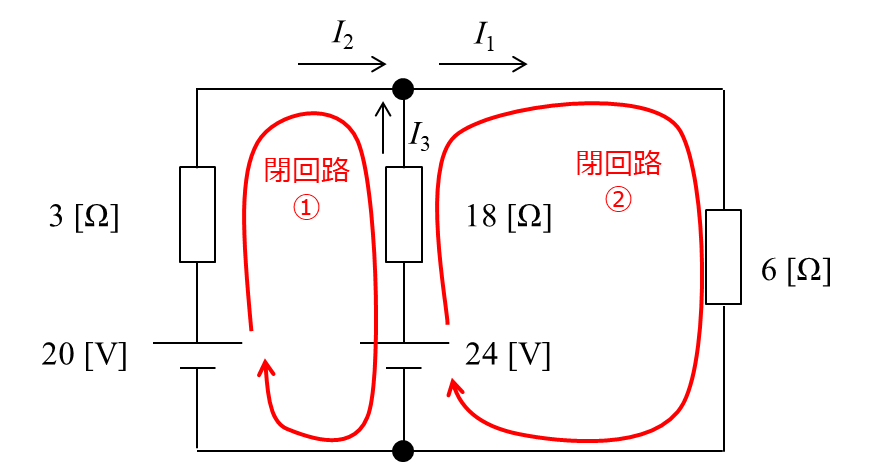
(2)へ(1)を代入します。
$$\begin{eqnarray} -4&=&3(I_1-I_3)-18I_3 \\ -4&=&-21I_3+3I_1 \tag{4}\\ \end{eqnarray}$$(3)に7/6をかけて、(3)と(4)で連立させます。
$$\begin{eqnarray} \left\{ \begin{array}{l} 28&=&21I_3+7I_1 \\ -4&=&-21I_3+3I_1 \end{array} \right. \end{eqnarray}$$この2式で足し算を行い、I1について整理します。
$$\begin{eqnarray} 24&=&10I_1 \\ I_1&=&\frac{24}{10} \\ &=&2.4\rm{[A]} \end{eqnarray}$$したがって、6[Ω]に加わる電圧Vは、オームの法則より以下で求められます。
$$\begin{eqnarray} V=6\times2.4=14.4\rm{[V]} \end{eqnarray}$$