問題
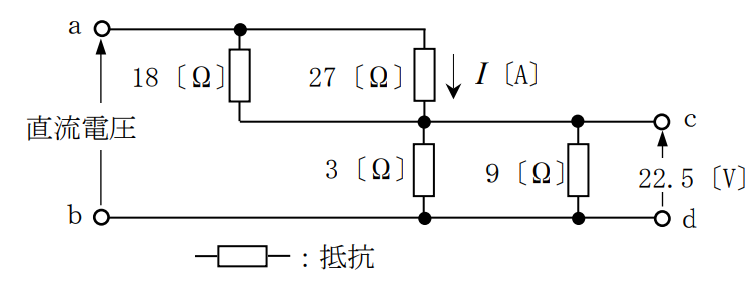
図に示す回路において、端子ab間に直流電圧を加えたところ、端子cd間に22.5 [V]の電圧が現れた。27 [Ω]の抵抗に流れる電流Iの値として、正しいものを下の番号から選べ。
- 1.4[A]
- 2.6[A]
- 3.8[A]
- 4.0[A]
- 5.2[A]
解答
4
解説
直流回路の直並列接続
問題の回路は一見複雑に見えますが、下記の様に書き換えることができます。
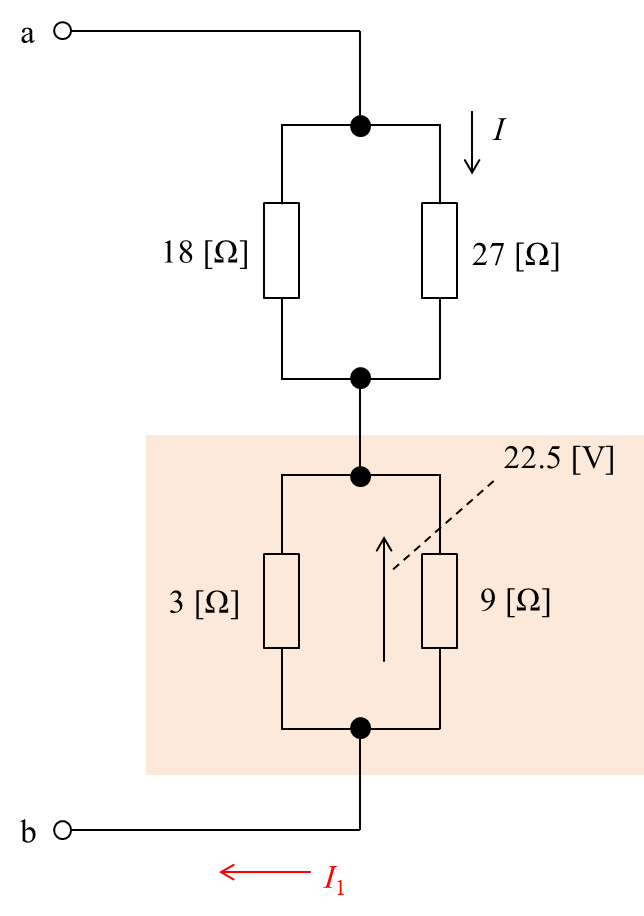
まず、回路全体に流れる電流I1を求めます。
網掛けの部分の合成抵抗R2は、
$$\begin{eqnarray} R_2=\frac{3\times9}{3+9}=\frac{27}{12}=\frac{9}{4}[\rm \Omega] \end{eqnarray}$$したがって、回路全体に流れる電流I1は、
$$\begin{eqnarray} I_1=\frac{4\times22.5}{9}=\frac{90}{9}=10[\rm A] \end{eqnarray}$$と求められます。
続いて、上側の並列接続された抵抗の合成抵抗Rを求めます。
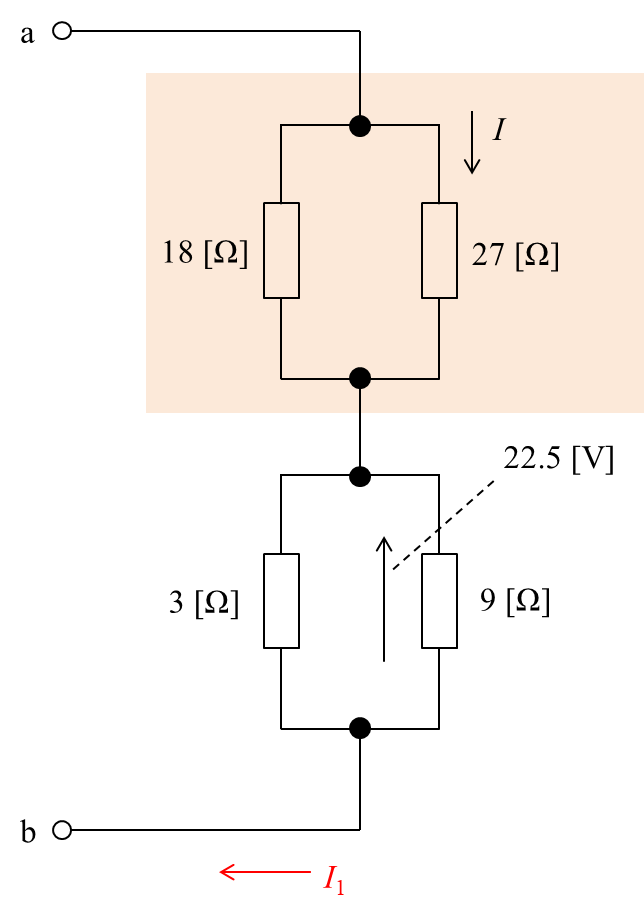
したがって、この並列抵抗に加わる電圧Vは、
$$\begin{eqnarray} V&=&RI_1=\frac{54}{5}\times 10\\ &=&108[\rm V] \end{eqnarray}$$と求められます。
したがって、電流Iは下記の様に求めることができます。
$$\begin{eqnarray} I&=&\frac{108}{27}\\ &=&\frac{36}{9}\\ &=&4.0[\rm A] \end{eqnarray}$$