問題
図に示すように、送信機の出力電力を17 [dB]の減衰器を通過させて電力計で測定したとき、その指示値が10 [mW]であった。この送信機の出力電力の値として、最も近いものを下の番号から選べ。ただし、log102=0.3とする。

- 350 [mW]
- 500 [mW]
- 900 [mW]
- 1,500 [mW]
- 2,000 [mW]
解答
2
解説
対数の計算
この問題は、下記の様に、デシベルに換算して計算します。
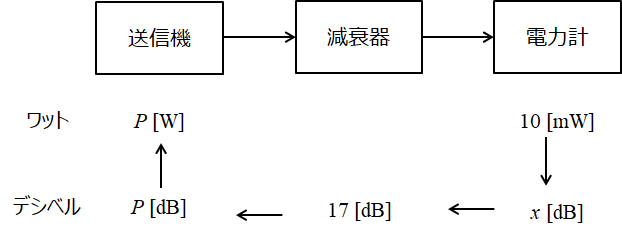
まず、10[mW]をデシベルに直します。
$$\begin{eqnarray} x[\rm{dB}]=10\log_{10}(10\times10^{-3})=-20[\rm{dB}] \end{eqnarray}$$元の送信電力から17[dB]減衰させたのが-20[dB]なので、送信電力P[dB]は、
$$\begin{eqnarray} P[\rm{dB}]=-20+17=-3[\rm{dB}] \end{eqnarray}$$と計算できます。したがって、送信電力P[dB]は下記の様に表すことができます。
$$\begin{eqnarray} -3[\rm{dB}]&=&10\log_{10}P \\ 0.3&=&-\log_{10}P \end{eqnarray}$$よって、送信電力P[W]は下記の様に求められます。
$$\begin{eqnarray} 0.3=-\log_{10}P&=&\log_{10}2 \\ \log_{10}P&=&-\log_{10}2=\log_{10}2^{-1} \\ P&=&\frac{1}{2}=0.5[\rm{W}]=500[\rm{mW}] \end{eqnarray}$$別解:[dBm]を使った方法
10[mW]をデシベルに直すとき、10-3をつけずに計算します。
$$\begin{eqnarray} x[\rm{dB}]=10\log_{10}10=10[\rm{dBm}] \end{eqnarray}$$これは1[mW]を基準としてlogをとっており、この方法をdBmといいます。
よって、送信電力P[dB]は、
$$\begin{eqnarray} P[\rm{dBm}]=10+17=27[\rm{dBm}] \end{eqnarray}$$と計算できます。したがって、送信電力P[mW]は下記の様に求められます。
$$\begin{eqnarray} 27[\rm{dBm}]&=&10\log_{10}P \\ 2.7&=&\log_{10}P \\ 2.7&=&3-0.3 \\ &=&\log_{10}10^3-\log_{10}2 \\ &=&\log_{10}\frac{10^3}{2}=\log_{10}500\\ P&=&500[\rm{mW}] \\ \end{eqnarray}$$