電気通信主任技術者 令和6年第1回 電気通信システム問2

問題

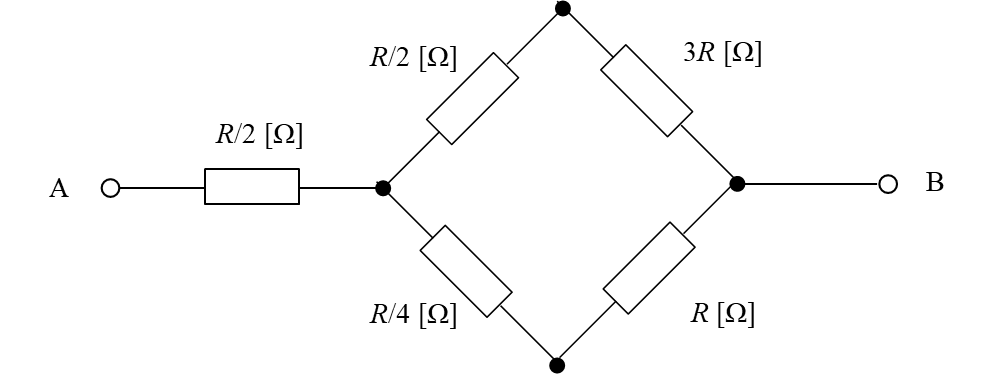
図に示す回路において、端子A-B間の合成抵抗は、(　　)[Ω]である。

1. 8
2. 19
3. 26
4. 27
5. 38

解答

4

解説

不平衡なブリッジ回路であるため、Δ-Y変換を用いて解きます。

以下のような回路において、各抵抗は次の関係が成り立ちます。

$$\begin{eqnarray} R_a&=&\frac{R_1R_3}{R_1+R_2+R_3} \\ R_b&=&\frac{R_1R_2}{R_1+R_2+R_3} \\ R_c&=&\frac{R_2R_3}{R_1+R_2+R_3} \\ \end{eqnarray}$$

R=19[Ω]として、Ra、Rb、Rcを求めます。

$$\begin{eqnarray} R_a&=&\frac{R\times2R}{R+2R+R}=\frac{R}{2} \\ R_b&=&\frac{2R\times R}{R+2R+R}=\frac{R}{2} \\ R_c&=&\frac{R\times R}{R+2R+R}=\frac{R}{4} \\ \end{eqnarray}$$

したがって、問題の回路は、次のように書き換えられます。

抵抗の直並列回路となり、合成抵抗R₀[Ω]は、次のように求められます。

$$\begin{eqnarray} R_0&=&\frac{R}{2}+\frac{\left(\frac{R}{2}+3R\right)\times\left(\frac{R}{4}+R\right)}{\frac{R}{2}+3R+\frac{R}{4}+R} \\ &=&\frac{R}{2}+\frac{\left(R+6R\right)\times\left(R+4R\right)}{4R+24R+2R+8R} \\ &=&\frac{R}{2}+\frac{35}{38}R \\ &=&\frac{19R+35R}{38} \\ &=&\frac{54R}{38} \\ &=&\frac{54\times19}{38} \\ &=&27 [\Omega] \end{eqnarray}$$