問題
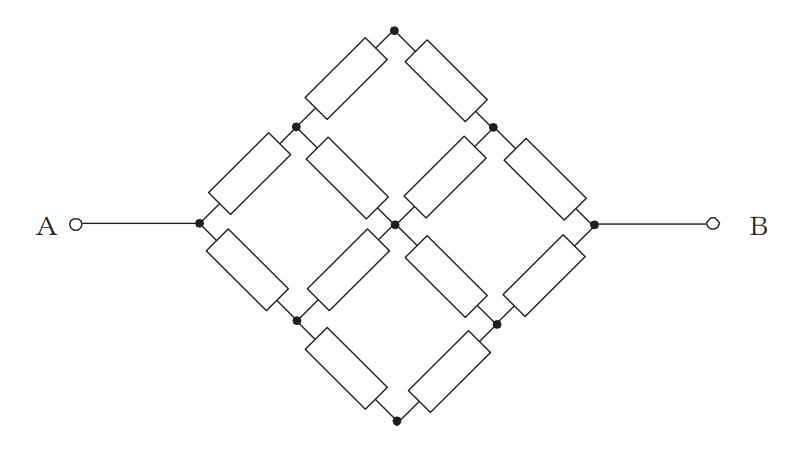
図に示す12個の抵抗によって構成された回路において、各抵抗の値が全て同一の2.0[Ω]であるとき、端子A-B間の合成抵抗は、( )[Ω]である。
- 2.0
- 2.5
- 3.0
- 3.5
- 4.0
解答
3
解説
この問題は解き方が2つあります。
解き方1:キルヒホッフの法則を使う方法
回路全体に流れる電流をIとすると、各接点に流入する電流と流出する電流は等しいので、各抵抗に流れる電流を下図のように書くことができます。

続いて、AB間の経路1つを考えます。

回路全体の電圧と各抵抗で発生する電圧の和は等しいため、合成抵抗R0、各抵抗R、Iを用いて、全体の電圧Vは下記のように展開できます。
$$\begin{eqnarray} V=R_0I=\frac{1}{2}RI+\frac{1}{4}RI+\frac{1}{4}RI+\frac{1}{2}RI \end{eqnarray}$$この式を整理して、R0について解きます。
$$\begin{eqnarray} R_0I&=&\frac{1}{2}RI+\frac{1}{4}RI+\frac{1}{4}RI+\frac{1}{2}RI \\ &=&RI+\frac{1}{2}RI \\ R_0&=&\frac{3}{2}R \end{eqnarray}$$R=2.0[Ω]を代入すると、R0を求めることができます。
$$\begin{eqnarray} R_0&=&\frac{3}{2}\times2.0=3\rm{[\Omega]} \\ \end{eqnarray}$$解き方2:回路の対称性を使う方法
もう一つの解き方として、回路の対称性を用いる方法があります。
線対称な回路は、単純化な並列回路に置き換える事ができる、という性質を持ちます。
さらに、線対称な回路は、対称となる回路を、独立して切り離してしまうことができます。

では、この2つの性質を使って、問題を解いてみます。
まず、問題の回路について、対称となる回路を分けてみます。

この赤の部分を取り出すと、下記のような直並列回路として見ることができます。

抵抗をRとして、合成抵抗R1を求めます。
$$\begin{eqnarray} R_1&=&R+\frac{2R\times2R}{2R+2R}+R \\ &=&2R+R \\ &=&3R \end{eqnarray}$$したがって、問題文の回路は、下記の回路に置き換えることができます。
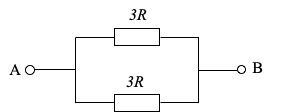
合成抵抗R0を下記のように求めます。
$$\begin{eqnarray} R_0&=&\frac{3R\times3R}{3R+3R} &=&\frac{3}{2}R \end{eqnarray}$$R=2.0[Ω]を代入して、R0を求めます。
$$\begin{eqnarray} R_0&=&\frac{3\times2.0}{2}=3\rm{[\Omega]} \end{eqnarray}$$