一陸特 令和2年2月 無線工学(B)問3

問題

図に示す回路の端子ab間の合成静電容量の値として、正しいものを下の番号から選べ。

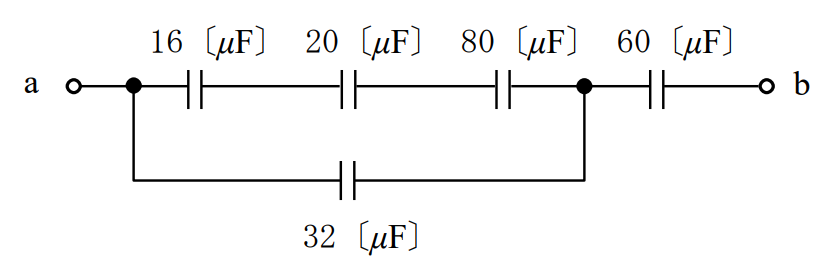
1. 12 [μF]
2. 16 [μF]
3. 20 [μF]
4. 24 [μF]
5. 30 [μF]

解答

4

解説

コンデンサの合成容量

コンデンサの合成容量は直列接続、並列接続それぞれ、下記の様に求められます。

$$直列接続の合成容量\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}$$ $$並列接続の合成容量C=C_1+C_2$$

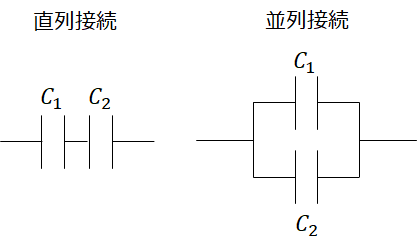
この公式を用いて、まずは、3つの直列接続部分の合成容量C_Aを求めます。

$$\begin{eqnarray} \frac{1}{C_A}&=&\frac{1}{16\times10^{-6}}+\frac{1}{20\times10^{-6}}+\frac{1}{80\times10^{-6}} \\ &=&\frac{5}{80\times10^{-6}}+\frac{4}{80\times10^{-6}}+\frac{1}{80\times10^{-6}} \\ &=&\frac{10}{80\times10^{-6}} \\ &=&\frac{1}{8\times10^{-6}} \\ \end{eqnarray}$$

したがって、

$$C_A= 8 [\mu \rm F] $$

と求められます。等価回路図を描くと、下記の様になります。

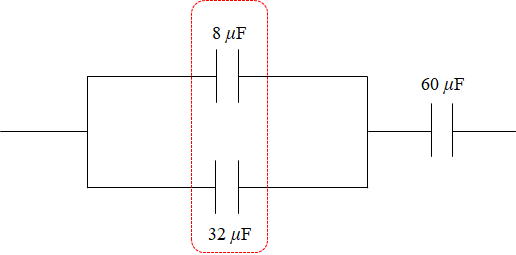
続いて、並列接続の合成容量C_Bを求めます。

$$\begin{eqnarray} C_B=8+32=40[\mu \rm F] \\ \end{eqnarray}$$

等価回路図は下記の様になります。

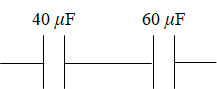
最後に、回路全体の合成容量C₀を求めます。

$$\begin{eqnarray} \frac{1}{C_0}&=&\frac{1}{40}+\frac{1}{60} \\ &=&\frac{3}{120}+\frac{2}{120} \\ &=&\frac{5}{120} \\ &=&\frac{1}{24} \\ \end{eqnarray}$$

これより、

$$C_0 = 24 [\mu \rm F] $$

と求められます。