問題
図に示すように、一辺がr[Ω]の電熱線で作った正方形の対角線をそれぞれ同じ線種の電熱線で結んだ回路のa-b間の合成抵抗値は、( )[Ω]である。

解答
4
解説
この問題は、解き方として、回路の対称性を用いて解きます。
回路の対称性とは何なのでしょうか?
線対称な回路は、下記のような単純化な抵抗の並列接続に置き換える事ができる、という性質を持ちます。

では、この性質を使って問題を解いてみます。
まず、問題の回路について、対称となる部分を下記のように分けてみます。
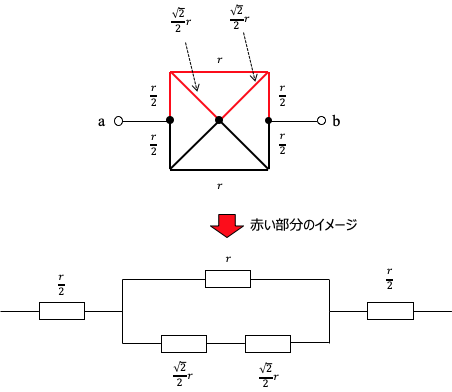
赤の部分を取り出すと、このような直並列回路として見ることができます。
この取り出した部分の合成抵抗R1を求めます。
$$\begin{eqnarray} R_1&=&\frac{r}{2}+\frac{r\times \left( \frac{\sqrt{2}}{2}r+\frac{\sqrt{2}}{2}r \right)}{r+\frac{\sqrt{2}}{2}r+\frac{\sqrt{2}}{2}r}+\frac{r}{2} \\ &=&r+\frac{r\times \sqrt{2}r}{r+\sqrt{2}r}\\ &=&r+\frac{\sqrt{2}r}{\sqrt{2}+1}\\ &=&r+\frac{\sqrt{2}r\left(\sqrt{2}-1\right)}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}\\ &=&r+2r-\sqrt{2}r\\ &=&\left(3-\sqrt{2}\right)r\\ \end{eqnarray}$$したがって、問題文の回路は、下記の回路に置き換えることができます。
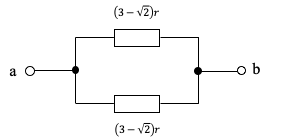
合成抵抗R0を下記のように求めます。
$$\begin{eqnarray} R_0&=&\frac{\left(3-\sqrt{2}\right)r\times\left(3-\sqrt{2}\right)r}{\left(3-\sqrt{2}\right)r+\left(3-\sqrt{2}\right)r} \\ &=&\frac{3-\sqrt{2}}{2}r \end{eqnarray}$$