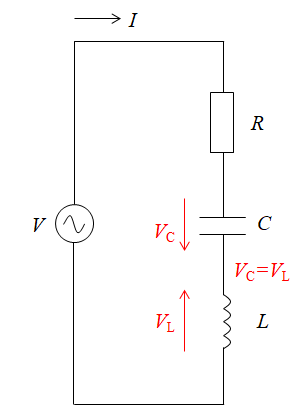
問題
図に示す直列共振回路において、Rの両端の電圧VR及びXCの両端の電圧VXC の大きさの値の組合せとして、正しいものを下の番号から選べ。ただし、回路は、共振状態にあるものとする。
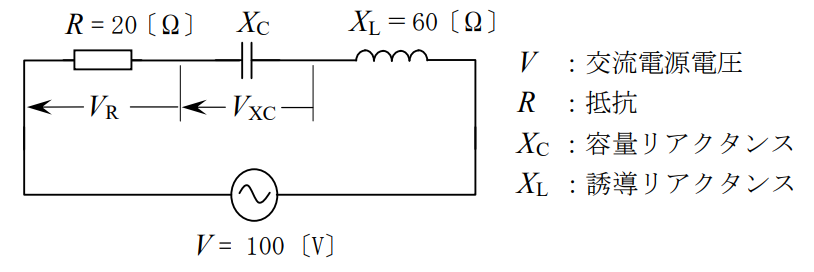
| VR | VXC | |
|---|---|---|
| 1 | 50[V] | 150[V] |
| 2 | 50[V] | 300[V] |
| 3 | 100[V] | 150[V] |
| 4 | 100[V] | 300[V] |
| 5 | 100[V] | 450[V] |
解答
4
解説
RLC直列共振回路の計算
共振状態のとき、コイルLとコンデンサCをないものとして考えられるため、抵抗に加わる電圧VRは電源電圧と等しく、100[V]です。
また、回路全体の電流Iを求めます。
$$\begin{eqnarray} I=\frac{V}{R}=\frac{100}{20}=5 [\rm A] \end{eqnarray}$$これより、コイルに加わる電圧VXLは、
$$\begin{eqnarray} V_{XL}=X_LI=60\times5=300 [\rm V] \end{eqnarray}$$と求められます。
また、コンデンサに加わる電圧VXCと、コイルに加わる電圧VXLは等しいので、
$$\begin{eqnarray} V_{XC}=V_{XL}=300 [\rm V] \end{eqnarray}$$と求められます。
RLC直列共振回路の解説
下記のRLC直列回路について、合成インピーダンスZを求めます。
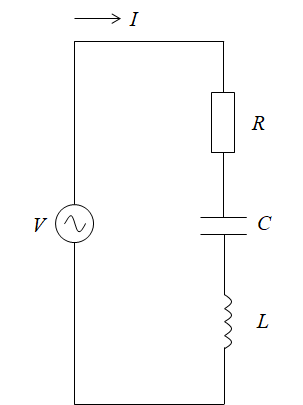
したがって、回路に流れる電流Iは、
$$\begin{eqnarray} \dot{I}=\frac{\dot{V}}{\dot{Z}}=\frac{\dot{V}}{R+j\left(\omega L -\frac{1}{\omega C}\right)} \end{eqnarray}$$となり、実効値で表すと、複素数の絶対値の公式から、
$$\begin{eqnarray} I&=&|\dot{I}|=\frac{|\dot{V}|}{\left|R+j\left(\omega L -\frac{1}{\omega C}\right)\right|} \\ &=&\frac{V}{\sqrt{R^2+\left(\omega L-\frac{1}{\omega C}\right)^2}} \end{eqnarray}$$と求めることができます。
ここで、ωL-1/ωC=0のときを考えてみましょう。すると、
$$\begin{eqnarray} I&=&\frac{V}{\sqrt{R^2+\left(\omega L-\frac{1}{\omega C}\right)^2}} \\ &=&\frac{V}{R} \\ \end{eqnarray}$$と書くことができます。
これは、ωL-1/ωC=0のときには、RLC直列回路はコイルLとコンデンサCをないものとして、単なる抵抗Rだけの回路と同じである、と言えるのです。
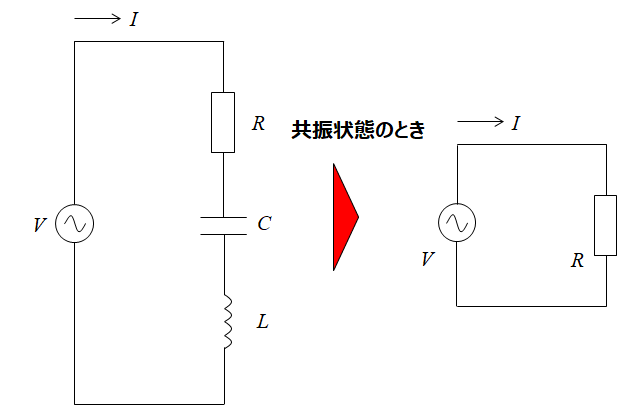
このωL-1/ωC=0のときを共振状態といいます。
共振状態のとき、実際には、コンデンサCとコイルLに電圧が加わっていないというわけではなく、同じ大きさで逆位相となり、互いに打ち消しあっています。