問題
次の記述は、パルスレーダーの最小探知距離について述べたものである。( )内に入れるべき字句の正しい組合せを下の番号から選べ。
- (1):最小探知距離は、主としてパルス幅に( A )する。
- (2):したがって、受信機の帯域幅を( B )し、パルス幅を( C )するほど近距離の目標が探知できる。
| A | B | C | |
|---|---|---|---|
| 1 | 反比例 | 広く | 狭く |
| 2 | 反比例 | 狭く | 広く |
| 3 | 比例 | 広く | 狭く |
| 4 | 比例 | 狭く | 広く |
| 5 | 比例 | 広く | 広く |
解答
3
解説
レーダー(Radar)
レーダーはある対象となる物体までの距離や方向を測る装置で、電波をその物体に向けて発射し、その反射波によって距離や方向を測定します。

レーダーの最小探知距離
レーダーが物体を探せる最小の距離の事で、これより短い距離の物体は見つけることができません。
最小探知距離は主にパルス幅、垂直方向の指向性によって決まります。
ここでは、問題文中のパルス幅について考えてみます。

最小探知距離とパルス幅

結論としては、最小探知距離を短くするには、パルス幅も狭くする必要があります。
また、f=1/Tの関係より、パルス幅を狭くするほど周波数帯域幅も大きくなります。
では、なぜパルス幅が狭いほど、探知できる距離を短くできるのでしょうか?
答えとしては、レーダーでは送信アンテナと受信アンテナを共用しているため、電波を送信している時間が短いほど、すぐに受信へ切り替えることができるからです。
というのも、電波を送信している間はレーダーのアンテナは送信アンテナとして用いられているため、物体からの反射波を受信できないのです。
そのため、パルス幅が狭い、つまり電波の送信期間が短いと、最小探知距離を短くできます。
例:パルス幅が100[μs]の場合
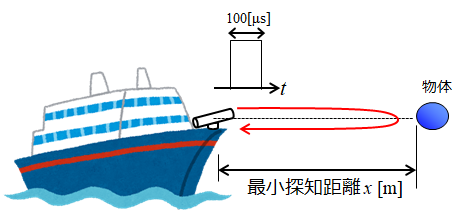
距離x=速さ×時間の関係式を用いて計算します。
電波の速さは光速と同じ3.0×108 [m/s]、時間は100[μs]、距離は往復で2倍かかるため、
$$\begin{eqnarray} 2x&=&(3.0\times10^8)\times(100\times10^{-6})\\ x&=&1.5\times10^4\\ &=&15[\rm km] \end{eqnarray}$$と求めることができます。
例:パルス幅が10[μs]の場合
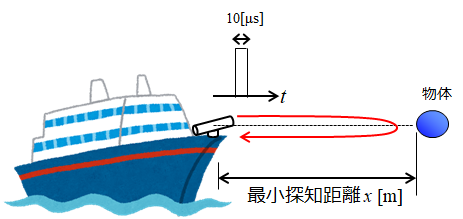
同様に、電波の速さ3.0×108 [m/s]、時間は10[μs]を用いると、
$$\begin{eqnarray} 2x&=&(3.0\times10^8)\times(10\times10^{-6})\\ x&=&1.5\times10^3\\ &=&1.5[\rm km] \end{eqnarray}$$と求めることができます。
このように、パルス幅が短いほど、最小探知距離を短くできるのです。