問題
次の記述は、図1及び図2に示す共振回路について述べたものである。このうち誤っているものを下の番号から選べ。ただし、ω0[rad/s]は共振角周波数とする。
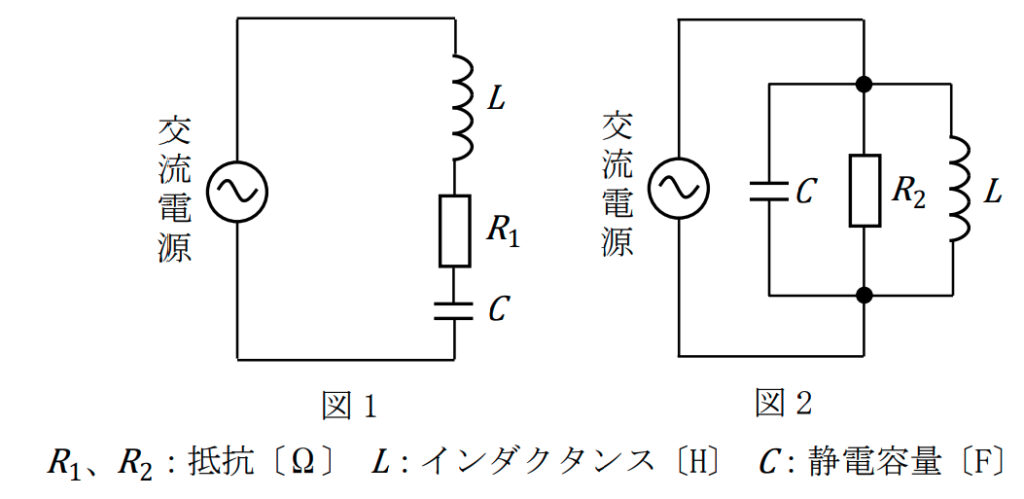
- 図1の共振時の回路の合成インピーダンスは、R1である。
- 図1の共振回路のQ(尖鋭度)は、Q=ω0CR1である。
- 図2の共振角周波数ω0は、ω0=1/√LCである。
- 図2の共振回路のQ(尖鋭度)は、Q=R2/ω0Lである。
解答
2
解説
RLC直列共振回路
下記のRLC直列回路について、合成インピーダンスZを求めます。

従って、回路に流れる電流Iは、
$$\begin{eqnarray} \dot{I}=\frac{\dot{V}}{\dot{Z}}=\frac{\dot{V}}{R+j(\omega L-\frac{1}{\omega C})} \end{eqnarray}$$となり、実効値で表すと、複素数の絶対値の公式から、
$$\begin{eqnarray} I&=&|\dot{I}|=\left| \frac{\dot{V}}{R+j(\omega L-\frac{1}{\omega C})} \right| \\ &=&\frac{V}{\left| R+j(\omega L-\frac{1}{\omega C})\right|} \\ &=&\frac{V}{\sqrt{R^2+(\omega L-\frac{1}{\omega C})^2}} \end{eqnarray}$$と書くことができます。
ここで、電流Iが最大になるのは、分母が最も小さいとき、すなわちωL-1/ωC=0のときです。

この状態を共振といいます。
RLC直列回路において共振状態になるには、ωL-1/ωC=0を満たすときなので、この時の角周波数をω0とすると、
$$\begin{eqnarray} \omega_0 L-\frac{1}{\omega_0 C}&=&0 \\ \omega_0 L&=&\frac{1}{\omega_0 C} \\ \omega_0^2LC&=&1 \\ \omega_0^2&=&\frac{1}{LC} \\ \omega_0 &=& \frac{1}{\sqrt{LC}} \\ 2\pi f_0 &=& \frac{1}{\sqrt{LC}} \\ f_0 &=& \frac{1}{2 \pi \sqrt{LC}} \\ \end{eqnarray}$$と求めることができます。この時の周波数f0を共振周波数といいます。
また、共振の鋭さを表すQ値があり、最大値I0と1/√2となるときの周波数幅の比で定義されています。
また、Q値は展開すると、下記式で求められることが知られています。
$$\begin{eqnarray} Q=\frac{f_0}{f_2-f_1}=\frac{\omega_0 L}{R}=\frac{1}{\omega_0 CR} \end{eqnarray}$$
RLC並列共振回路
RLC並列回路でも同様に計算します。

共振周波数f0は
$$\begin{eqnarray} f_0 &=& \frac{1}{2 \pi \sqrt{LC}} \\ \end{eqnarray}$$と求めることができ、またQ値は
$$\begin{eqnarray} Q=\frac{f_0}{f_2-f_1}=\omega_0 CR=\frac{R}{\omega_0 L} \end{eqnarray}$$にて求めることができます。