一陸特 令和3年10月 無線工学(A)問4

問題

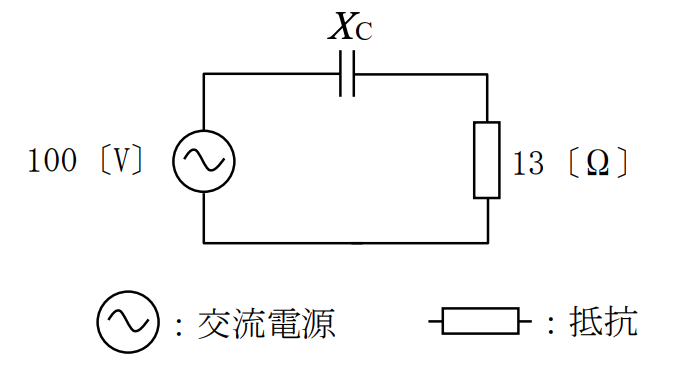
図に示す直列回路において消費される電力の値が520[W]であった｡このときのコンデンサのリアクタンスX_C[Ω]の値として､正しいものを下の番号から選べ｡

1. 5[Ω]
2. 9[Ω]
3. 13[Ω]
4. 18[Ω]
5. 24[Ω]

解答

2

解説

コンデンサでは電力を消費せず、電力は抵抗だけで発生します。

したがって、P=VI=RI²の関係が成り立ち、これを電流I[A]について整理します。

$$\begin{eqnarray} P&=&RI^2 \\ I&=&\sqrt{\frac{P}{R}} \\ &=&\sqrt{\frac{520}{13}} \\ &=&\sqrt{40} \\ \end{eqnarray}$$

また、RC直列回路の合成インピーダンスZ[Ω]は、下記のように求められます。

$$\begin{eqnarray} Z&=&\sqrt{R^2+X_C^2} \\ \end{eqnarray}$$

ここで、Zは下記のようにもかけます。

$$\begin{eqnarray} Z&=&\frac{V}{I} \end{eqnarray}$$

これらの関係を整理します。

$$\begin{eqnarray} Z=\frac{V}{I}&=&\sqrt{R^2+X_C^2} \\ \frac{V^2}{I^2}&=&R^2+X_C^2 \\ X_C^2&=&\frac{V^2}{I^2}-R^2 \\ &=&\frac{10000}{40}-13^2 \\ &=&250-169 \\ &=&81\\ X_C&=&9 \end{eqnarray}$$

合成インピーダンス

交流RLC直列回路において、抵抗をR[Ω]、コイルのリアクタンスをX_L[Ω]、コンデンサのリアクタンスをX_C[Ω]としたとき、合成インピーダンスZ[Ω]は下記の式で求められます。

$$\begin{eqnarray} Z&=&\sqrt{R^2+(X_L-X_C)^2} \end{eqnarray}$$