問題
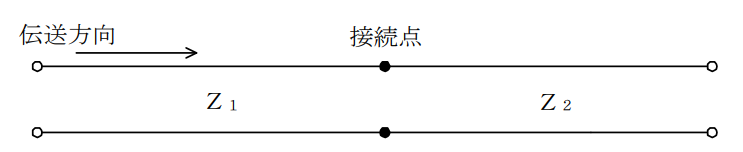
図に示すように、特性インピーダンスがZ1の伝送ケーブルに特性インピーダンスZ2の伝送ケーブルを接続したとき、その接続点における電圧反射係数は、( )で表される。
解答
1
解説
反射係数の公式より、Z0=Z01[Ω]、ZL=Z02[Ω]として、電圧反射係数Γは下記のように求められます。
$$\begin{eqnarray} \Gamma&=&\frac{Z_L-Z_0}{Z_L+Z_0}\\ &=&\frac{Z_{2}-Z_{1}}{Z_{1}+Z_{2}}\\ \end{eqnarray}$$反射係数
異なる特性インピーダンスの伝送路同士を接続すると、反射波といって、信号の一部が戻ってきてしまい、電力損失が発生します。

入射波と反射波の電圧の割合を電圧反射係数または反射係数といい、下記式で表されます。
$$\begin{eqnarray} \Gamma=\frac{V_r}{V_i}=\frac{Z_L-Z_0}{Z_L+Z_0} \end{eqnarray}$$Viは入射波の電圧、Vrは反射波の電圧を表します。
ZL=Z0となっている状態を整合といい、整合している時に反射波が0となり、反射係数も0となります。
同様に、入射波と反射波の電流の割合を電流反射係数といい、入射波の電流をIi、反射波の電流Irとすると、電流反射係数Γiは下記のように表されます。
$$\begin{eqnarray} \Gamma _i=\frac{I_r}{I_i}=-\Gamma \end{eqnarray}$$