問題
次の記述は、等価地球半径について述べたものである。このうち正しいものを下の番号から選べ。ただし、大気は標準大気とする。
- 電波は電離層のE層の電子密度の不均一による電離層散乱によって遠方まで伝搬し、実際の地球半径に散乱域までの地上高を加えたものを等価地球半径という。
- 大気の屈折率は、地上からの高さとともに減少し、大気中を伝搬する電波は送受信点間を弧を描いて伝搬する。この電波の通路を直線で表すため、仮想した地球の半径を等価地球半径という。
- 地球の中心から静止衛星までの距離を半径とした球を仮想したとき、この球の半径を等価地球半径という。
- 等価地球半径は、真の地球半径を3/4倍したものである。
解答
2
解説
見通し距離と等価地球半径
下図のA点とB点があった場合、お互いが見通せる距離の範囲dは、下記の様に算出できることが知られています。
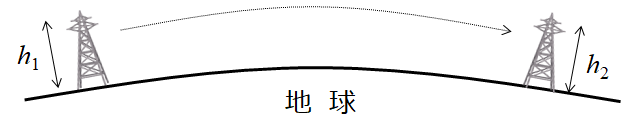
等価地球半径係数K=1のとき
$$d\simeq 3.57(\sqrt{h_1}+\sqrt{h_2})$$等価地球半径係数K=4/3のとき
$$d\simeq 4.12(\sqrt{h_1}+\sqrt{h_2})$$このdを超えると、見通しがなくなるために電波が届かなくなり、通信を行うことが困難になってしまいます。
ここで、等価地球半径係数Kとは何なのでしょうか?
これは、実際の伝搬状況を考慮した補正係数を意味しています。

というのも、実際の電波伝搬は、大気中での屈折があるため、直線的な伝搬よりさらに遠くへ伝搬します。
この実際の伝搬状況について、2点間の距離を直線として表すためには、実際の地球より半径を4/3倍します。これを等価地球半径といい、この計数を等価地球半径計数と言います。
大気中での屈折を考慮しない場合がK=1、考慮する場合がK=4/3となっています。