一陸特 令和7年6月 無線工学(B)問4

問題

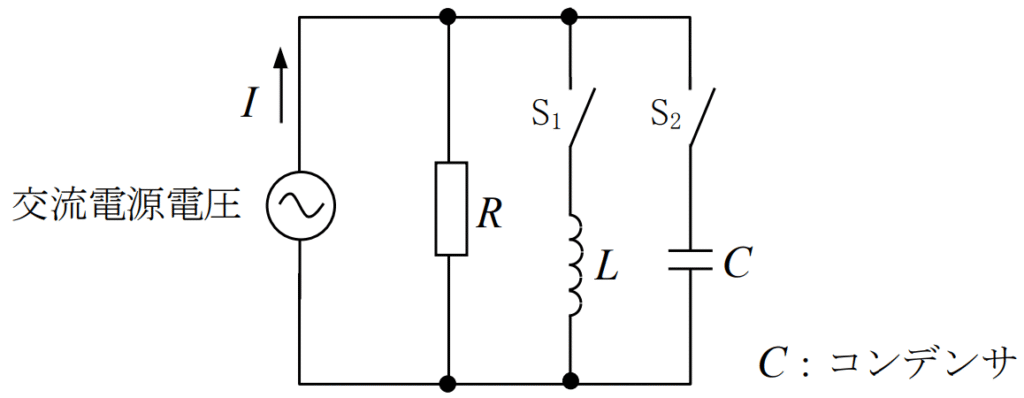
図に示す回路において、スイッチS₁のみを閉じたときの電流IとスイッチS₂のみを閉じたときの電流Iは、ともに5[A]であった。また、スイッチS₁とS₂の両方を閉じたときの電流Iは、4[A]であった。抵抗R及びコイルLのリアクタンスX_Lの値の組合せとして、正しいものを下の番号から選べ。ただし、交流電源電圧は150[V]とする。

	R	XC
1	18.2 [Ω]	30[Ω]
2	18.2 [Ω]	50[Ω]
3	18.2 [Ω]	75[Ω]
4	37.5 [Ω]	50[Ω]
5	37.5 [Ω]	75[Ω]

解答

4

解説

RLC並列回路の計算

スイッチS₁を閉じた場合とスイッチS₂を閉じた場合で電流が等しいため、コイルのリアクタンスX_LとコンデンサのリアクタンスX_Cの間には、下記の関係が成り立ちます。

$$\begin{eqnarray} X_L=X_C \end{eqnarray}$$

続いて、スイッチを両方閉じたときの合成インピーダンスZ₀を求めます。

$$\begin{eqnarray} \dot{Z_0}&=&\frac{1}{\frac{1}{R}+\frac{1}{jX_L}+j\frac{1}{X_C}} \\ &=&\frac{RX_LX_C}{X_LX_C-jRX_C+jRX_L} \\ Z_0=|\dot{Z_0}|&=&\frac{|RX_LX_C|}{\left|X_LX_C+j\left(X_L-X_C\right)\right|} \\ &=&\frac{RX_LX_C}{\sqrt{X_L^2X_C^2+\left(X_L-X_C\right)^2}} \\ \end{eqnarray}$$

電流4[A]、電圧150[V]、X_L=X_Cの関係を用いて、上の式をさらに展開します。

$$\begin{eqnarray} Z_0=\frac{150}{4}&=&\frac{RX_LX_C}{\sqrt{X_L^2X_C^2+\left(X_L-X_C\right)^2}} \\ 37.5&=&\frac{RX_C^2}{\sqrt{X_C^4}} \\ 37.5&=&\frac{RX_C^2}{X_C^2} \\ R&=&37.5 [\Omega] \end{eqnarray}$$

また、スイッチS₂だけを閉じた場合について、合成インピーダンスZ₂を求めます。

$$\begin{eqnarray} \dot{Z_2}&=&\frac{1}{\frac{1}{R}+j\frac{1}{X_C}} \\ &=&\frac{RX_C}{X_C+jR} \\ Z_2=|\dot{Z_2}|&=&\frac{|RX_C|}{|X_C+jR|} \\ &=&\frac{RX_C}{\sqrt{R^2+X_C^2}} \\ \end{eqnarray}$$

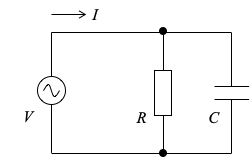
電流5[A]、電圧150[V]、抵抗R=37.5[Ω]なので、下記のように展開できます。

$$\begin{eqnarray} Z_2=\frac{150}{5}&=&\frac{RX_C}{\sqrt{R^2+X_C^2}} \\ 30&=&\frac{37.5\times X_C}{\sqrt{37.5^2+X_C^2}} \\ 30^2&=&\frac{37.5^2\times X_C^2}{37.5^2+X_C^2} \\ 30^2\left(37.5^2+X_C^2\right)&=&37.5^2X_C^2 \\ \frac{75^2}{2^2}X_C^2-30^2X_C^2-30^2\times\frac{75^2}{2^2}&=&0 \\ \frac{5625-3600}{4}X_C^2--\frac{30^2\times75^2}{4}&=&0 \\ 2025X_C^2-30^2\times75^2&=&0 \\ \left(45X_C-30\times75\right)\left(45X_C+30\times75\right)&=&0 \\ \end{eqnarray}$$

X_C>0なので、X_Cは下記のように求められます。

$$\begin{eqnarray} 45X_C-30\times75&=&0\\ 9X_C-6\times75&=&0\\ 3X_C-2\times75&=&0\\ X_C-2\times25&=&0\\ X_C&=&50 \\ \end{eqnarray}$$