問題
大気中において、等価地球半径係数KをK=1としたときの、球面大地での見通し距離dを求める式として、正しいものを下の番号から選べ。ただし、h1[m]及びh2[m]は、それぞれ送信及び受信アンテナの地上高とする。
- d≒3.57(√h1+√h2) [km]
- d≒3.57(h12+h22) [km]
- d≒4.12(√h1+√h2) [km]
- d≒4.12(h12+h22) [km]
解答
1
解説
見通し距離
下図のA点とB点があった場合、お互いが見通せる距離の範囲dは、下記の様に算出できることが知られています。
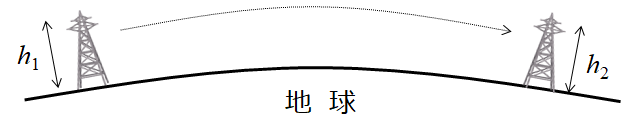
等価地球半径係数K=1のとき
$$d\simeq 3.57(\sqrt{h_1}+\sqrt{h_2})$$等価地球半径係数K=4/3のとき
$$d\simeq 4.12(\sqrt{h_1}+\sqrt{h_2})$$このdを超えると、見通しがなくなるために電波が届かなくなり、通信を行うことが困難になってしまいます。
ここで、等価地球半径係数Kとは何なのでしょうか?
これは、実際の伝搬状況を考慮した補正係数を意味しています。

というのも、実際の電波伝搬は、大気中での屈折があるため、直線的な伝搬よりさらに遠くへ伝搬します。
この大気中での屈折を考慮しない場合がK=1、考慮する場合がK=4/3となっています。