問題
図に示すマイクロ波回線において、A局から送信機出力電力0.4[W]で送信したときのB局の受信機入力電力の値として、最も近いものを下の番号から選べ。ただし、自由空間基本伝送損失を134[dB]、送信及び受信アンテナの絶対利得をそれぞれ39[dB]、送信及び受信帯域フィルタ(BPF)の損失をそれぞれ1[dB]、送信及び受信給電線の長さをそれぞれ15[m]とし、給電線損失を0.2[dB/m]とする。また、1[mW]を0[dBm]、log102=0.3とする。
- -30[dBm]
- -32[dBm]
- -34[dBm]
- -36[dBm]
- -38[dBm]
解答
5
解説
まず、送信機出力を対数[dBm]に変換します。
電力P[mW]を[dBm]に変換するには、以下の式を使います。
$$\begin{eqnarray} [\rm{dBm}]=10\log_{10}{(P{\rm{[mW]}})}\\ \end{eqnarray}$$これを用いて、送信機出力Pt[dBm]を求めます。
$$\begin{eqnarray} P_t&=&10\log_{10}(400)\\ &=&10\log_{10}{(2^2\times10^2)} \\ &=&20\log_{10}{2}+10\log_{10}{10^2}\\ &=&20\times0.3+20\\ &=& 26 [\rm{dBm}]\\ \end{eqnarray}$$問題文で与えられた損失と利得をまとめると、以下の図のようになります。
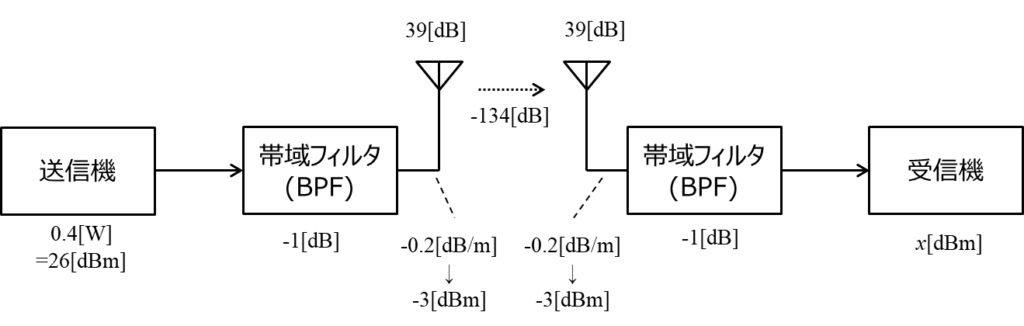
したがって、受信機の入力電力x[dBm]は以下で求められます。
$$\begin{eqnarray} x&=&26-1-3+39-134+39-3-1\\ &=&-38 [\rm{dBm}]\\ \end{eqnarray}$$距離減衰
電波はどこまでも届くわけではなく、通信できる範囲が限られます。というのも、送信機から受信機が遠ければ遠いほど、電波が弱くなっていくからです。これを距離減衰といいます。
特に、距離減衰の中でも自由空間での距離減衰を自由空間伝搬損失といいます。
自由空間とは、送信機と受信機の間に障害物や反射が無く、電波が直接伝搬するような環境をいいます。自由空間伝搬損失Γ0は下記式で求められます。
$$\begin{eqnarray} \Gamma _0 = \left(\frac{4\pi d}{\lambda}\right)^2 \end{eqnarray}$$