一陸特 令和4年10月 無線工学(A)問7

問題

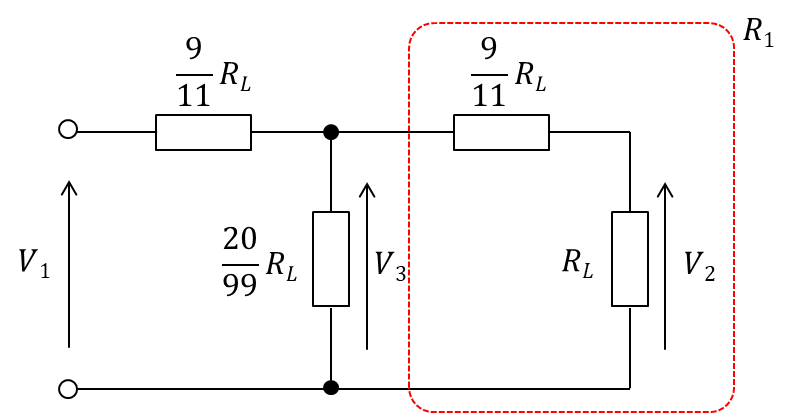
図に示すT形抵抗減衰器の減衰量Lの値として、最も近いものを下の番号から選べ。ただし、減衰量Lは、減衰器の入力電力をP₁、入力電圧をV₁、出力電力をP₂、出力電圧をV₂とすると、次式で表されるものとする。また、log₁₀2＝0.3とする。

L＝10log₁₀(P₁/P₂)＝10log₁₀{(V₁²/R_L)/(V₂²/R_L)} [dB]

1. 3 [dB]
2. 6 [dB]
3. 9 [dB]
4. 14 [dB]
5. 20 [dB]

解答

5

解説

T形抵抗減衰器

まず、赤色の部分の合成抵抗R₁を求めます。

$$\begin{eqnarray} R_1=\frac{9}{11}R_L+R_L=\frac{20}{11}R_L \end{eqnarray}$$

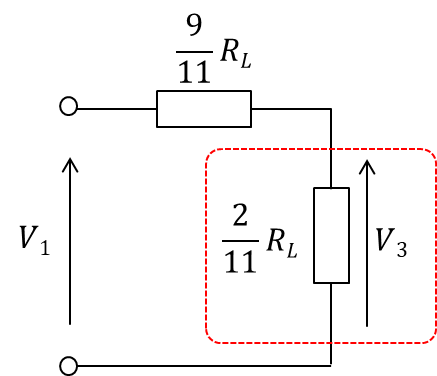
続いて、赤色の部分の合成抵抗R₂を求めます。

$$\begin{eqnarray} R_2&=&\frac{\frac{20}{99}R_L\times\frac{20}{11}R_L}{\frac{20}{99}R_L+\frac{20}{11}R_L} \\ &=&\frac{\frac{20\times20}{99\times11}R_L^2}{\frac{200}{99}R_L} \\ &=&\frac{20\times20\times99R_L^2}{99\times11\times200R_L} \\ &=&\frac{20}{11\times10}R_L \\ &=&\frac{2}{11}R_L \\ \end{eqnarray}$$

今求めた合成抵抗R₂に加わる電圧V₃を求めます。

$$\begin{eqnarray} V_3&=&\frac{\frac{2}{11}R_L}{\frac{9}{11}R_L+\frac{2}{11}R_L}V_1 \\ &=&\frac{2}{11}V_1 \\ \end{eqnarray}$$

続いて、電圧V₂を求めます。

$$\begin{eqnarray} V_2&=&\frac{R_L}{\frac{9}{11}R_L+R_L}V_3 \\ &=&\frac{1}{\frac{20}{11}}\times\frac{2}{11}V_1 \\ &=&\frac{1}{10}V_1 \\ \end{eqnarray}$$

最後に、電圧V₂を減衰量Lの式に代入します。

$$\begin{eqnarray} L&=&10\log_{10}{\frac{\frac{V_1^2}{R_L}}{\frac{V_2^2}{R_L}}}=10\log_{10}{\frac{V_1^2}{V_2^2}} \\ &=&10\log_{10}{\frac{V_1^2}{\frac{1}{10^2}V_1^2}} \\ &=&10\log_{10}{10^2} \\ &=&20\log_{10}{10} \\ &=&20 [\rm dB] \end{eqnarray}$$