一陸特 令和3年10月 無線工学(B)問6

問題

図に示すように、内部抵抗rが10[Ω]の交流電源に、負荷抵抗R_Lを接続したとき、R_Lから取り出しうる電力の最大値(有能電力)として、正しいものを下の番号から選べ。ただし、交流電源の起電力Eは100[V]とする。

1. 100[W]
2. 250[W]
3. 400[W]
4. 600[W]
5. 750[W]

解答

2

解説

まず、R_Lでの電力Pを求めます。

$$\begin{eqnarray} I&=&\frac{E}{r+R_L}\\ P&=&R_LI^2=\frac{E^2}{(r+R_L)^2}R_L \end{eqnarray}$$

ここで、電力が最大となるのは、r=R_Lのときです。

この関係より、最大有能電力P_maxは下記のように求められます。

$$\begin{eqnarray} P_{max}&=&\frac{E^2}{(2r)^2}r \\ &=&\frac{E^2}{4r} \\ &=&\frac{100^2}{4\times10} \\ &=&\frac{10000}{40} \\ &=&250 \end{eqnarray}$$

最大有能電力

下記のように、内部抵抗r、電圧Vの電圧源に、負荷抵抗Rが接続された回路を考えます。

負荷抵抗Rでの電力が最大となるのは、r=Rのときということが知られています。

これを供給電力最大の法則といいます。

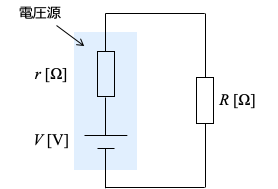
また、その時の電力P_maxを最大有能電力や最大電力といい、下記で求めることができます。

$$\begin{eqnarray} P_{max}&=&\frac{V^2}{4r} \\ \end{eqnarray}$$