問題
半波長ダイポールアンテナに対する相対利得が12[dB]の八木・宇田アンテナ(八木アンテナ)から送信した最大放射方向にある受信点の電界強度は、同じ送信点から半波長ダイポールアンテナに8[W]の電力を供給し送信したときの、最大放射方向にある同じ受信点の電界強度と同じであった。このときの八木・宇田アンテナ(八木アンテナ)の供給電力の値として、最も近いものを下の番号から選べ。ただし、アンテナの損失はないものとする。また、log102=0.3とする。
- 0.1[W]
- 0.125[W]
- 0.25[W]
- 0.5[W]
- 1.0[W]
解答
4
解説
八木・宇田アンテナと相対利得
八木・宇田アンテナについて、半波長ダイポールアンテナに対する相対利得は、下記の式で求められます。
$$\begin{eqnarray} G=10\log_{10}{\frac{P}{P_y}} [\rm dB] \end{eqnarray}$$ここで、Pyは八木・宇田アンテナでの電力[W]、Pは半波長ダイポールアンテナの電力[W]を表しています。
相対利得を求めるときには、同じ距離・同じ受信点で、同じ電界強度同士でなければなりません。
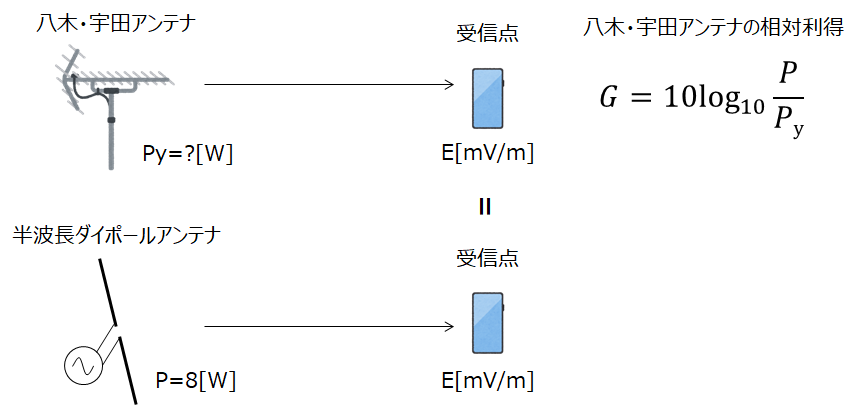
八木・宇田アンテナの相対利得の式に、値を代入します。
$$\begin{eqnarray} 12&=&10\log_{10}{\frac{8}{P_y}} \\ 1.2&=&\log_{10}{8}-\log_{10}{P_y} \\ \log_{10}{P_y}&=&\log_{10}{8}-1.2 \\ &=&\log_{10}{8}-4\times\log_{10}{2}\\ &=&\log_{10}{8}-\log_{10}{2^4}\\ &=&\log_{10}{\frac{8}{16}}\\ &=&\log_{10}{0.5}\\ P_y&=&0.5[\rm W] \end{eqnarray}$$