問題
次の記述は、図に示すマイクロ波回線の第1フレネルゾーンについて述べたものである。( )内に入れるべき字句の正しい組合せを下の番号から選べ。
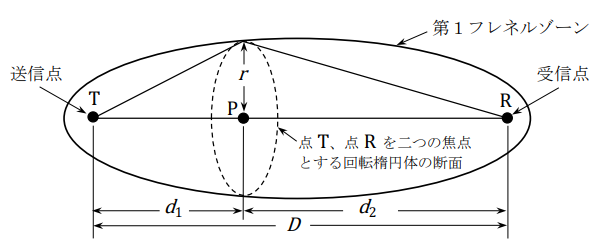
- (1):送信点Tから受信点R方向に測った距離d1[m]の点Pにおける第1フレネルゾーンの回転楕円体の断面の半径r[m]は、点Pから受信点Rまでの距離をd2[m]、波長をλ[m]とすれば、次式で与えられる。
r≒( A ) - (2):周波数が7.5[GHz]、送受信点間の距離Dが15[km]であるとき、d1が6[km]の点Pにおけるrは、約( B )である。
| A | B | |
|---|---|---|
| 1 | √(λd1/(d1+d2)) | 6[m] |
| 2 | √(λd1/(d1+d2)) | 8[m] |
| 3 | √(λd1d2/(d1+d2)) | 10[m] |
| 4 | √(λd1d2/(d1+d2)) | 12[m] |
| 5 | √(λd1d2/(d1+d2)) | 14[m] |
解答
4
解説
計算方法
まず、2点間の距離Dが15[km]、d1が6[km]なので、d2は下記のように求められます。
$$\begin{eqnarray} D&=&d_1+d_2 \\ d_2&=&D-d_1\\ &=&15-6\\ &=&9[\rm{km}] \end{eqnarray}$$第1フレネルゾーンの計算式に数値を代入します。
$$\begin{eqnarray} r&=&\sqrt{\frac{\lambda d_1 d_2}{d_1+d_2}}\\ &=&\sqrt{\frac{c}{f}\times\frac{d_1 d_2}{d_1+d_2}} \\ &=&\sqrt{\frac{3.0\times 10^8}{7.5\times 10^9}\times\frac{(6\times 10^3) \times (9 \times 10^3)}{(6+9)\times 10^3}} \\ &=&\sqrt{\frac{3.0}{75}\times\frac{54000}{15}} \\ &=&\sqrt{\frac{3.0}{75}\times\frac{10800}{3}} \\ &=&\sqrt{\frac{10800}{75}} \\ &=&\sqrt{\frac{2160}{15}} \\ &=&\sqrt{\frac{432}{3}} \\ &=&\sqrt{144} \\ &=&12[\rm m] \end{eqnarray}$$フレネルゾーン
送信機から受信機へ電波を送信する際、その間に障害物がなく、送信側から受信側まで直接、電波を届けられる環境を見通し(LOS; Line Of Sight)があるといいます。
見通し内通信、見通し内伝搬、見通しが良い、などともいうことがありますが、すべて同じ意味です。
このように、障害物による反射が無く、送信機から受信機へ直接電波を届けられる環境を自由空間と言います。
反対に、遮蔽物で遮られる場合は見通し外(NLOS; Non Line Of Sight)通信、といいます。(同様に、見通し外伝搬、見通しが悪い、などとも言います)
では、送受信機間に、どの程度遮蔽物が存在したら、見通し内もしくは見通し外と判別されるのでしょうか?
この分ける目安となるのが、フレネルゾーンという考え方です。
第1フレネルゾーン内に障害物が無ければ、見通し内通信と言ってよいでしょう。
というのも、第1フレネルゾーンの中にある遮蔽物によって、伝搬損失がほぼ決まってしまうからです。

フレネルゾーンとは、送信側と受信側を結ぶ線を回転軸とした、楕円体の範囲のことを言います。
なぜフレネルゾーンという考え方があるのかというと、電波は送信側と受信側へまっすぐ進むだけでなく、その周囲に広がりを持って伝搬するからです。
特に、送信側と受信側の最短距離d+λ/2までの範囲にある楕円体を、第1フレネルゾーンと言います。

フレネルゾーンの大きさを決める短軸の長さr[m]は、次の式で求められることが知られています。
$$\begin{eqnarray} r=\sqrt{\frac{\lambda d_1 d_2}{d_1+d_2}}=\sqrt{\frac{c}{f}\times\frac{d_1 d_2}{d_1+d_2}} \end{eqnarray}$$これより、短軸の長さrは、周波数が大きくなるほどは小さくなることが分かります。